Серединный треугольник и прямая Эйлера

А что вы можете сказать про треугольники SABA` и SAA`C?

Если провести такие же рассуждения, то получим, что y = z.

Какой можно сделать вывод из 2 последних рассуждений?

x = y = z.

Прекрасно вы показали, что x = y = z.

Теорема 3.1: Треугольник делится своими медианами на шесть меньших треугольников равной площади. Запчасти на мопед альфа запчасти мопед альфа воронеж.

Далее ученикам сообщается уже известный факт.

Продолжая рассмотрение рисунка, отмечаем, что SGAB = 2SGBA`. Так как эти треугольники имеют общую высоту, то отсюда следует, что |AG|=2|GA`|. Аналогично, |BG|=2|GB`| и |CG|=2|GC`|.

Теорема 3.2: Медианы треугольника делят одна другую в отношении 2:1.

Другими словами, каждая медиана отсекает треть другой.

Чевианы AD, BE, CF, перпендикулярные прямым BC, CA, AB, соответственно, называются высотами треугольника АВС. Теорема, обратная теореме Чевы, устанавливает их конкурентность. Их общая точка Н называется ортоцентром.

Ученики записывают определение

Сами точки D, E, F называются основаниями высот. Соединяя их попарно, мы получим треугольник DEF – ортотреугольник треугольника АВС.

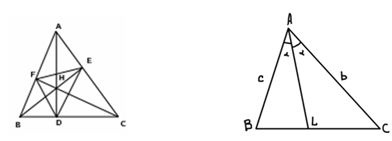
Следующий блок информации дается учителем, ученики записывают теоремы, определения и делают чертежи.

Другое важное семейство чевиан образуют биссектрисы внутренних углов. На рисунке показана одна такая биссектриса AL.

В данный момент можно попросить учеников сформулировать теорему 1.1 и спросить – почему ее можно применить в данном случае?

Применяя теорему 1.1 к двум треугольникам ABL и ALC (углы которых в точке L, равные синусы), мы получаем:

.

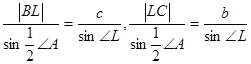Так как можем получить аналогичные результаты для биссектрис внутренних углов B и C, то таким образом доказали.

Теорема 3.3: Каждая биссектриса внутреннего угла в треугольнике делит противоположную сторону на отрезки, длины которых пропорциональны длинам прилегающих сторон.

Следующие три момента нужно отдельно выделить, после их предварительного воспроизведения учащимися.

Любая точка на прямой AL равноудалена от прямых CA и AB. Аналогично, любая точка на биссектрисе внутреннего угла В равноудалена от прямых ВА и ВС. Следовательно, точка I, в которой эти две биссектрисы пересекаются, находится на равных расстояниях r от трех сторон:

Из последнего вывода делается вывод (он хорошо известен учащимся из курса планиметрии и проверен на практике, заодно можно вспомнить понятие конкурентности).

Теорема 3.4: Биссектрисы трех внутренних углов треугольника конкурентны.

Окружность с центром в точке I и радиуса r касается всех трех сторон и поэтому является вписанной окружностью.

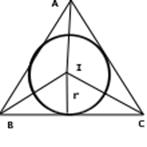
Решение задач:

1. В остроугольном треугольнике АВС высоты АА1 и ВВ1 пересекаются в точке О. Найдите угол ОВА, если угол ОСА = 38°.

2. В треугольнике АВС биссектрисы ВВ1 и СС1 пересекаются в точке О. Найдите отношение площадей треугольника ВОА и АОС, если АВ = 10, АС = 15.

3. В остроугольном треугольнике АВС серединные перпендикуляры сторон АВ и АС пересекаются в точке О и ОА = 8. Найдите площадь треугольника ОВС, если угол ОВС = 60°.

4. В остроугольном треугольнике АВС высоты ВВ1 и СС1 пересекаются в точке О. Найдите угол ОАВ, если ВС = 2ВС1.

5. В треугольнике АВС медианы ВВ1 и СС1 пересекаются в точке О и взаимно перпендикулярны. Найдите ОА, если ВВ1 = 36, СС1 = 15.

Домашнее задание:

Решить задачи:

1. В остроугольном треугольнике АВС серединные перпендикуляры сторон ВС и АС пересекаются в точке О. Найдите строну Ос, если АВ = 10, а угол ВОА = 120°.

2. Во внутренней области треугольника АВС взята точка О, равноудаленная от его сторон. Найдите угол АОС, если угол АВО = 39°.

3. Найдите углы треугольника, если известно, что одна из биссектрис этого треугольника разбивают его на два равнобедренных треугольника.

Доделать задачи, которые не сделаны на уроке.

Подготовить доклад на тему «Вневписанная окружность»

4.2.4 Вписанная и вневписанная окружности

Этап 1. Проверка домашнего задания.

Познавательно о обучении:

Изучение развития музыкально-творческих способностей дошкольников во всех видах музыкальной деятельности
Анализ использования разных видов непосредственно образовательной музыкальной деятельности 1. Программное содержание. Программное содержание и задачи, поставленные педагогом на данном занятии по каждому виду музыкальной деятельности — слушанию музыки, пению, музыкально-ритмическим движениям, игре н ...

Позиционно-дидактическая концепция
В основу модели личностно-ориентированного образования, разработанной В.В. Сериковым, положена идея С.Л. Рубинштейна, согласно которой сущность личности проявляется в ее способности занимать определенную позицию. Личность – это не набор заданных качеств, а способность человека «быть личностью», то ...

Особенности проведения занятий при заболеваниях центральной и периферической нервной системы
При заболеваниях и травмах нервной системы в процессе занятий физическими упражнениями учитель должен учитывать такие особенности состояния организма, как: - повышенная ранимость нервной системы по отношению к физичес-ким (удары, сотрясения, растяжения, перезагибание) и психическим (умственным и эм ...