Серединный треугольник и прямая Эйлера

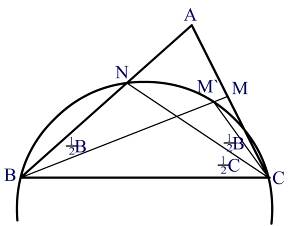
Доказательство теоремы 6.1:

При доказательстве этой теоремы важно обратить внимание учащихся на построении структуры логических рассуждений, которые делают доказательство данной теоремы более коротким.

Часто случается, что теорема может быть выражена в форме «противоположной к обратной» – эквивалентной первоначальной.

Например, вместо того, чтобы сказать: «Все люди смертны», мы можем также сказать «Бессмертные не есть люди».

Вместо доказательства самой теоремы 6.1. нам достаточно доказать, что если в треугольнике АВС: , то . Но это есть прямое следствие леммы 6.1.2.

Теорема 6.2: Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

Учащимся предлагается самостоятельно показать доказательство этой теоремы дома.

Мы уже отметили на рисунке, что . А так как отрезок HD перпендикулярен отрезку DB, то и отрезок FD должен быть перпендикулярен отрезку OB. Перпендикулярность отрезков DE и OC, а также EF и OA показывается аналогично.

Решение задач:

Задачи 1-7 из задачника.

Домашнее задание:

Решить задачи 8-11 из задачника.

Этап 1. Проверка домашнего задания. Особое внимание уделяется проверке доказательства теоремы 6.2.

Этап 2. Повторение ранее изученного материала. Проводится сначала письменный опрос учащихся по материалу предыдущих уроков. После окончания работы ученики сдают листочки со своими ответами, и начинается устный опрос по тем же самым вопросам, что дает возможность учащимся проверить их работы.

Этап 3. Введение нового материала.

Учащиеся записывают определение:

Треугольник, полученный соединением середин сторон данного треугольника, назовем серединным треугольником.

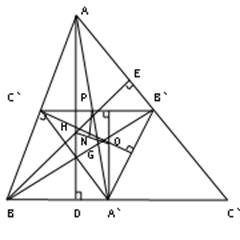
На доске по заготовленному за ранее чертежу ведется объяснение.

На рисунке A`B`C` есть срединный треугольник треугольника АВС. Рассмотрим так же две медианы AA` и BB`, пересекающиеся в точке G, две высоты треугольника ABC, пересекающиеся в точке H, и две высоты треугольника A`B`C` пересекающиеся в точке O.

Что вы можете сказать про треугольники АВС и А`B`C`? Какие они?

Стороны треугольника A`B`C` параллельны сторонам треугольника АВС, поэтому эти треугольники подобны.

Далее, |C`B`|=1/2|BC|, поэтому отношение длин любых двух соответствующих отрезков (а не только соответствующих сторон) будет равно1:2. В действительности, отрезки B`C`, C`A`, A`B` разбивают треугольник ABC на четыре конгруэнтных треугольника. Кстати, точка P –середина отрезка B`C` – также является и серединой отрезка AA`

Далее мы видим, что AC`A`B` – параллелограмм, следовательно, прямая AA` делит пополам отрезок B`C`. Поэтому медианы треугольника A`B`C` лежат на медианах треугольника ABC, а это значит, что оба треугольника имеют один и тот же центроид G.

Высоты треугольника A`B`C`, изображенные на рисунке, являются срединными перпендикулярами сторон AB и BC треугольника ABC. Отсюда делаем вывод, что точка O – ортоцентр треугольника A`B`C` – является время и центром окружности, описанной вокруг треугольника ABC.

Так как точка H – ортоцентр треугольника ABC, а точка O – ортоцентр подобного ему треугольника A`B`C`, то |AH| = 2 |OA`|. По теореме 3.2 |AG| + 2 |GA`|. И так как оба отрезка, AD и OA`, перпендикулярны стороне BC, то они параллельны. Следовательно,

ÐHAG = ÐOA`G, Ñ HAG ¥ Ñ OA`G и ÐAGH = Ð A`GO.

Этим показано, что точки O, G, H коллинеарны и |HG| = 2 |GO|, то есть справедлива

Теорема 7.1: Ортоцентр, центроид и центр описанной окружности произвольного треугольника лежат на одной прямой. Центроид делит расстояние от ортоцентра до центра описанной окружности в отношении 2:1.

Решение задач:

№55 из задачника.

Домашнее задание:

Учить все определения и теоремы.

Окружность девяти точек

Рассмотрим рисунок. На нем точки K, L, M – середины отрезков AH, BH, CH, лежащих на высотах.

Познавательно о обучении:

Трудности социализации детей сирот
В условиях воспитания в детском доме трудности, с которыми сталкивается ребенок в процессе социализации, удваивается. Это происходит потому, что сама организация жизнеспособности детей в детском доме устроена таким образом, что у ребенка формируется преимущественно только одна ролевая позиция - поз ...

Говорение как вид речевой деятельности. Понятие говорения
Основной целью обучения иностранному языку в школе в соответствии с требованиями, предъявляемыми обществом современному человеку, является формирование вторичной языковой личности, способной успешно осуществлять социальное взаимодействие с носителями иной культуры. Достижение данной цели невозможно ...

Метод моделирования как средства развития связной речи у старших дошкольников
Проблемой моделирования занимаются многие известные педагоги. В современной дидактической литературе распространено представление о моделировании как об одном из методов обучения, хотя, как научный метод моделирование известно, очень давно. В. А. Штофф определяет модель как «средство отображения, в ...