Серединный треугольник и прямая Эйлера

Этап 2. Введение нового материала.

Перед введением нового материала выслушивается доклад сделанный учениками по теме урока. В это время остальной класс делает конспект делаемого доклада. После завершения того, как доклад будет заслушан подводятся итоги по полученной информации и делаются выводы самими учениками под руководством учителя. А после этого уже сам учитель дополняет и корректирует материал текущего урока.

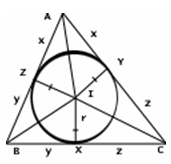
На рисунке изображена вписанная окружность, касающаяся сторон ВС, СА и АВ в точках X, Y, Z. Обозначим через x длины отрезков AY и AZ, через y длины отрезков BZ и BX, через z длины отрезков CX и CY.

Почему AY = AZ, BZ = BX, CX = CY?

Они равны. Так как две касательные к окружности, проведенные из внешней точки, равны, и мы получаем, что |AY|=|AZ|, |BZ|=|BX|, |CX|=|CY|.

На рисунке длины этих отрезков обозначены x, y, z так что y + z=a, z + x=b, x + y=c.

Сложим эти равенства. Что получим?

Получим 2x + 2y + 2z = a + b + c = Р, то есть периметр.

Для нужного нам обозначения используем введенное Эйлером обозначение s для полупериметра (от «semiperimetr»), получим 2x + 2y + 2z = a + b + c = 2s, поэтому х + y + z=s, т.е. справедлива

Теорема 4.1: Для треугольника, изображенного на рисунке, выполняются соотношения:

x=s-a,

y=s-b,

z=s-c.

Здесь x, y, z – длины равных отрезков касательных проведенных из точек А, В и С (А, В,С – вершины треугольника АВС) к окружности с центром в точке I и радиусом r, s – полупериметр треугольника АВС.

Дальнейшие рассуждения направлены на рассмотрение и доказательство следующей теоремы.

Рассмотрим треугольник IBC.

Чему равна площадь треугольника IBC с основанием а и высотой r?

Так как треугольник IBC имеет основание а и высоту r, то его площадь равна

А чему равны площади треугольников ICA и IAB?

Какое равенство будет получено, если сложить все три выражения для площадей треугольников IBC, ICA, IAB?

Мы получим: .

Тем самым вы доказали теорему.

Теорема 4.2: Для треугольника, изображенного на рисунке, выполняется соотношение:

SABC = sr.

Площадь треугольника АВС равна произведению полупериметра этого треугольника на радиус вписанной в него окружности.

Учащиеся под руководством учителя выполняют построения, фиксируют алгоритм построения и записывают следующие факты.

Построим произвольный остроугольный треугольник АВС. Продлим каждую из его сторон за вершины треугольника. Введем обозначения для продолжений сторон проведем дополнительные построения: а) построим биссектрисы внутренних треугольника и продлим их за стороны треугольника, б) построим биссектрисы внешних углов треугольника АВС, полученных продлением сторон треугольника за его вершины, в) точки пересечения биссектрис внутренних углов треугольника с соответствующими биссектрисами внешних углов обозначим как на рисунке, г) соединим полученные точки пересечения.

Мы получили изображение треугольника , стороны которого являются биссектрисами внешних углов треугольника АВС. Любая точка на биссектрисе угла В равноудалена от прямых АВ и ВС. Аналогично, любая точка на прямой равноудалена от прямых ВС и СА. Следовательно точка Ia, в которой эти биссектрисы пересекаются, находится на одинаковом расстоянии ra от всех трех сторон. Так как Ia равноудалена от сторон АВ и АС, то она должна принадлежать множеству точек, равноудаленных от этих прямых, то есть она должна лежать на прямой А1, внутренней биссектрисе угла А.

Теорема 4.3: Внешние биссектрисы любых двух углов треугольника конкурентны с внутренней биссектрисой третьего угла.

Для закрепления понимания понятия «конкурентности» у учащихся рекомендуется спросить расшифровку этого понятия.

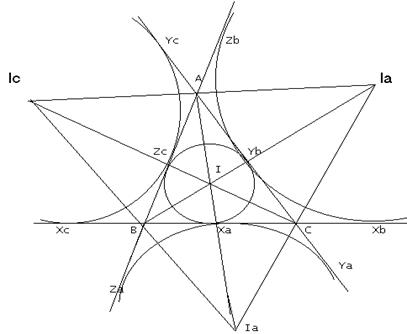
Окружность с центром в точке Ia радиуса ra, касающаяся всех трех сторон треугольника, является одной из трех вневписанных окружностей. Каждая из вневписанных окружностей касается одной из сторон треугольника внутри, а двух других сторон (продолженных) извне.

Познавательно о обучении:

Нормативно-правовая база патриотического воспитания
К настоящему времени уже сформирована определенная нормативно-правовая база патриотического воспитания. Имеются постановление Совета Министров РСФСР № 253 от 14 мая 1991 года "О допризывной подготовке учащейся молодежи в государственных общеобразовательных учебных заведениях РСФСР", Закон ...

Понятие о принципе наглядности. Исследования по данной проблеме
Учебная деятельность является важным содержанием особенно в младшем школьном возрасте. Под мотивацией учебной деятельности понимаются все факторы, обусловливающие проявление учебной активности: потребности, цели, установки, интересы. Матюхина М.В. указывает, что одно из важнейших условий формирован ...

Виды и формы деятельности
коллективно-творческие дела; игровые программы, игры, конкурсы, концерты; индивидуальные и групповые беседы; психологические тренинги; командная (отрядная) работа; работа в классах – мастерских; нетрадиционные формы работы. Основные службы, обеспечивающие полноценную жизнь Лагеря общения Педколлект ...