Серединный треугольник и прямая Эйлера

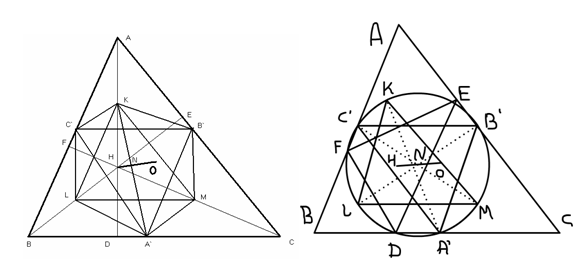
Так как BC – общая сторона двух треугольников ABC и HBC, а точки C`, B` и L, M являются серединами других их сторон соответственно, то отрезки C`B` и LM параллельны прямой BC. Аналогично, так как AH – общая сторона двух треугольников BAH и CAH, то оба отрезка C`L и B`M параллельны прямой AH. Следовательно, B`C`LM – параллелограмм. Так как отрезки BC и AH – перпендикулярны, то этот параллелограмм – прямоугольник. Аналогично, A`B`KL – прямоугольник. Следовательно, A`K, B`L, C`M являются тремя диаметрами окружности, как показано на рисунке.

Так как ÐA`DK – прямой, то эта окружность проходит через точку D. Точно также она проходит через точки E и F.

В итоге получаем:

Теорема 8.1. Основания трех высот произвольного треугольника, середины трех его сторон и середины трех отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности радиуса (Ѕ)R.

Теорема 8.2. Центр окружности девяти точек лежит на прямой Эйлера, точно в середине отрезка между ортоцентром и центром описанной окружности.

Решение задач:

Задача № 54, 56-58 из задачника.

Домашнее задание:

Решить задачи №№59-63.

Педальный треугольник

Ортотреугольник и серединный треугольник являются примерами сопутствующих треугольников более общего типа. Пусть Р – любая точка внутри данного треугольника АВС, и пусть из точки Р на стороны АВ, АС, ВС опущены перпендикуляры РA1, РB1, РС1. Треугольник, А1В1С1 вершинами которого являются основания этих перпендикуляров, называется педальным треугольником треугольника АВС для педальной точки Р.

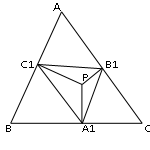
Теорема 9.1: Если расстояния от педальной точки до вершин треугольника АВС равны x, y, z, то длины сторон педального треугольника равны

В частном случае, когда , это утверждение общеизвестно.

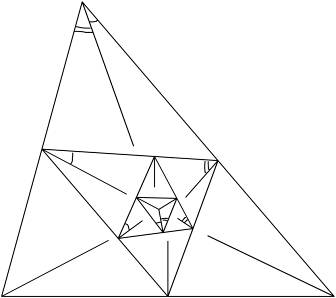
Теорема 9.2: Третий педальный треугольник подобен исходному.

Доказательство следует из чертежа.

Решение задач:

Задачи №36-41.

Домашнее задание:

Подготовиться к контрольной работе. Решить задачи №№ 16-25.

4.2.10 Контрольная работа

Данная контрольная работа состоит из 2 вариантов, каждый вариант содержит 4 задачи.

1. Вариант

1. Докажите, что биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной в этот треугольник окружности.

2. Докажите, что серединные перпендикуляры сторон треугольника пересекаются в одной точке, совпадающей с центром описанной около этого треугольника окружности.

3. Докажите, что биссектрисы внутреннего и внешнего углов при вершине С треугольника АВС равны тогда и только тогда, когда .

4. Дан треугольник АВС. Известно, что биссектриса СС1 внутреннего угла при вершине С равна биссектрисе СС2 внешнего угла при той же вершине. Может ли прямая СВ быть биссектрисой угла С1СС2?

2. Вариант

1. Докажите, что медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершин треугольника.

2. Докажите, что точка М, лежащая внутри треугольника АВС является точкой пересечения его медиан тогда и только тогда, когда треугольники АВМ, ВСМ, САМ равновелики.

3. Может ли центр описанной окружности треугольника АВС лежать на его: а) стороне, б) высоте, в) биссектрисе, г)средней линии?

4. Докажите, что в прямоугольном треугольнике медиана и высота, проведенные из вершины прямого угла, образуют равные углы с катетами.

Все предложенные задачи взяты из части «Задачи для самостоятельного решения» приложения (В1: №1 – 1, №2 – 2, №3 – 8, №4 – 9, В2: №1 –15, №2 – 16, №3 –20, №4 – 21).

Экспериментальная часть данной дипломной работы проводилась на базе ГОУ СОШ ЦО №1406, в десятых классах переводчиков и педагогов. В содержание апробации факультативного курса входило 12 занятий: по 9 основным темам, 2 занятия увеличенных по времени (1 занятие – 3 урока) специально отведенные для дополнительного решения задач и одно занятие – контрольная работа для проверки качества усвоения материала. Из каждого класса на факультативные занятия приходили практически все учащиеся. Надо отметить, что среди посещавших занятия учащихся был замечен огромный интерес к изучаемому материалу. Интерес учащихся выражался в их заинтересованности. Новизна изучаемого материала узнаваемого ими на основе уже имеющихся у них знаний и их новая интерпретация особенно нравилась ученикам. Учащиеся с огромным интересом делали чертежи предлагаемых теоретических фактов и решаемых на занятиях задач, и искали их модификации, а также выполняли задания направленные на их самостоятельную деятельность в подготовке исторических справок по изучаемому материалу. Еще один важный результат – учащиеся вне факультативных занятий, на уроках геометрии, искали пути применения новых знаний, и им это иногда очень успешно удавалось. Так же особый интерес у учащихся вызвало электронное сопровождение курса, специально для него разработанное. Электронное сопровождение курса особенно понравилось учащимся, так как в нем можно было самостоятельно создавать чертежи к содержанию занятий и произвольно их модифицировать, тем самым рассматривать различные случаи рассмотрения изучаемых фактов.

Познавательно о обучении:

Подбор игр для коррекции низкой двигательной активности
«Веселый мяч» Воспитатель предлагает детям представить, что они – мячики. Надо выполнять те движения, которые обычно используют в игре с мячом: прыжки, быстрый бег, перекатывание по полу и прочее. В конце игры отмечается, кто из детей придумал больше движений. Варианты игры: дети выполняют движения ...

Современные проблемы в преподавании русского языка
Перед обществом остро стоит проблема создания нормальной духовной среды для развития ребенка. Русский язык относится к тем предметам, результаты изучения которого и владение им определяются не только школьным обучением, но в значительной мере и обществом, в котором живет ребенок, окружающей его язы ...

Значение научных исследований
Современный специалист должен обладать глубокими знаниями и конструктивным мышлением. Чтобы стать специалистом, необходимо в совершенстве овладеть методологией научных исследований. Это позволит самостоятельно ставить и творчески решать сложные вопросы производства, сбыта и управления. Научная подг ...