Серединный треугольник и прямая Эйлера

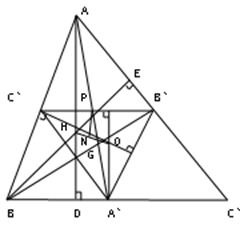
Треугольник, полученный соединением середин сторон данного треугольника, назовем серединным треугольником. На рисунке A`B`C` есть срединный треугольник треугольника АВС. Рассмотрим так же две медианы AA` и BB`, пересекающиеся в точке G, две высоты треугольника ABC, пересекающиеся в точке H, и две высоты треугольника A`B`C` пересекающиеся в точке O.

Во-первых, стороны треугольника A`B`C` параллельны сторонам треугольника АВС, поэтому эти треугольники подобны.

Далее, |C`B`|=1/2|BC|, поэтому отношение длин любых двух соответствующих отрезков (а не только соответствующих сторон) будет равно 1:2. В действительности, отрезки B`C`, C`A`, A`B` разбивают треугольник ABC на четыре конгруэнтных треугольника. Кстати, точка P –середина отрезка B`C` – также является и серединой отрезка AA`.

Далее мы видим, что AC`A`B` – параллелограмм, следовательно, прямая AA` делит пополам отрезок B`C`. Поэтому медианы треугольника A`B`C` лежат на медианах треугольника ABC, а это значит, что оба треугольника имеют один и тот же центроид G.

Высоты треугольника A`B`C`, изображенные на рисунке, являются срединными перпендикулярами сторон AB и BC треугольника ABC. Отсюда делаем вывод, что точка O – ортоцентр треугольника A`B`C` – является время и центром окружности, описанной вокруг треугольника ABC.

Так как точка H – ортоцентр треугольника ABC, а точка O – ортоцентр подобного ему треугольника A`B`C`, то |AH| = 2 |OA`|. По теореме 3.2. |AG| + 2 |GA`|. И так как оба отрезка, AD и OA`, перпендикулярны стороне BC, то они параллельны. Следовательно, ÐHAG = ÐOA`G, Ñ HAG ¥ Ñ OA`G и ÐAGH = Ð A`GO.

Этим показано, что точки O, G, H коллинеарны и |HG| = 2 |GO|, то есть справедлива.

Теорема 7.1: Ортоцентр, центроид и центр описанной окружности произвольного треугольника лежат на одной прямой. Центроид делит расстояние от ортоцентра до центра описанной окружности в отношении 2:1.

Окружность девяти точек

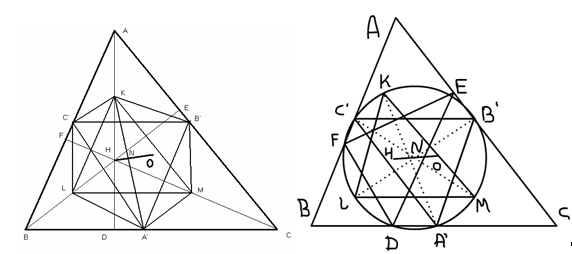
Рассмотрим рисунок. На нем точки K, L, M – середины отрезков AH, BH, CH, лежащих на высотах. Так как BC – общая сторона двух треугольников ABC и HBC, а точки C`, B` и L, M являются серединами других их сторон соответственно, то отрезки C`B` и LM параллельны прямой BC. Аналогично, так как AH – общая сторона двух треугольников BAH и CAH, то оба отрезка C`L и B`M параллельны прямой AH. Следовательно, B`C`LM – параллелограмм. Так как отрезки BC и AH – перпендикулярны, то этот параллелограмм – прямоугольник. Аналогично, A`B`KL – прямоугольник. Следовательно, A`K, B`L, C`M являются тремя диаметрами окружности, как показано на рисунке.

Так как ÐA`DK – прямой, то эта окружность проходит через точку D. Точно также она проходит через точки E и F.

Теорема 8.1: Основания трех высот произвольного треугольника, середины трех его сторон и середины трех отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности радиуса (Ѕ)R.

Теорема 8.2. Центр окружности девяти точек лежит на прямой Эйлера, точно в середине отрезка между ортоцентром и центром описанной окружности.

Педальный треугольник

Ортотреугольник и серединный треугольник являются примерами сопутствующих треугольников более общего типа. Пусть Р – любая точка внутри данного треугольника АВС, и пусть из точки Р на стороны АВ, АС, ВС опущены перпендикуляры РА1, РВ1, РС1. Треугольник, А1В1С1 вершинами которого являются основания этих перпендикуляров, называется педальным треугольником треугольника АВС для педальной точки Р.

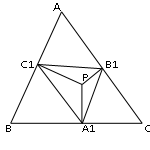
Теорема 9.1: Если расстояния от педальной точки до вершин треугольника АВС равны x, y, z, то длины сторон педального треугольника равны

В частном случае, когда , это утверждение общеизвестно.

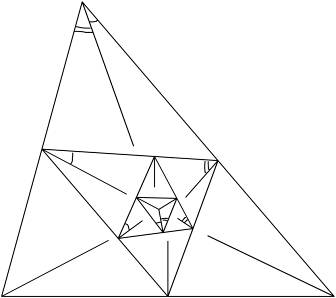
Теорема 9.2: Третий педальный треугольник подобен исходному.

Доказательство следует из чертежа.

Познавательно о обучении:

Педагогическая инновация - как научная категория
Хотя невозможно точно определить происхождение термина «инновация» (новшество), считается, что этот термин в общественные науки попал из естественных, поскольку прежде всего и в большом количестве новшества применяются в области агрономии, промышленности и медицины. Хотя инновации сопровождают обще ...

Чтение как процесс усвоения
Читатель не поглощает материал пассивно, как контейнер или губка. Это звучит банально, но вплоть до последнего времени авторитарные методы обучения, построенные на принципе кувшина и бутылки, господствовали в школе и за ее пределами, а традиция умирает медленно. Уважающий себя, независимый человек ...

Анализ Работы начальной школы
МОУ «Средняя общеобразовательная школа № 2 имени С.С. Орлова» ориентирована на обучение, воспитание и развитие всех и каждого учащегося с учетом индивидуальных (возрастных, физиологических, психологических, интеллектуальных и др.) особенностей, образовательных потребностей и возможностей, личностны ...