Общая характеристика дифференцированного зачета по теме: «Алгебраические дроби»

4. Довести учащихся до хорошего уровня усвоения знаний и способов деятельности.

С учащимися IV группы.

1. Ликвидация пробелов в знаниях и умениях.

2. Пробуждение интереса к предмету путем использования игровых элементов, занимательных и логических задач наряду с систематической организацией самостоятельной работы учащихся на уроке и дома.

3. Развитие навыков и умений осуществлять самостоятельную деятельность по образцу и в сходных ситуациях, воспроизводить изученный материал, решенную задачу.

Доведение учащихся до минимального уровня усвоения знаний и способов деятельности.

Задания для закрытого дифференцированного тематического зачета аналогичны заданиям, рассматриваемым в учебнике, то есть все задания учащимся знакомы. Этот зачет расчитан на один урок, и его проведение предполагается в конце изучения темы.

Для каждой группы учащихся, опираясь на цели обучения и уровень их подготовки, составлены задания для дифференцированного зачета. Каждой группе школьников предлагается 5 заданий, в которых есть задание на равенство дробей, приведение к общему знаменателю и различные действия с дробями.

Таким образом, разработанный дифференцированный зачет по теме: «Алгебраические дроби» является закрытым тематическим и содержит задания аналогичные заданиям из учебника.

Содержание закрытого дифференцированного тематического зачета по теме: «Алгебраические дроби»

I группа.

Составьте алгебраическую дробь, которая:

а) равна нулю при х=5 и не имеет смысла при х=10,

б) имела смысл при любом х. (4 балла)

Найдите х.

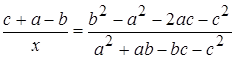. (3балла)

Упростите выражение: (11 баллов)

если x=.

Равносильны ли уравнения: (12 баллов)

x3-2x=0 и x3-.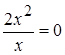

Докажите тождество: (18 баллов)

, если (a+b)(b+c)(a+c)=0.

II группа.

Составьте алгебраическую дробь, которая

а) равна нулю при х=а,

б) не имеет смысл при х=а-b. (4 балла)

При каких значениях переменной х равны значения алгебраических дробей: (4 балла)

, .

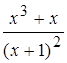Приведите дроби к общему знаменателю как можно более простого вида: (5 баллов)

, , .

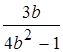Найдите значения выражения: (9 баллов)

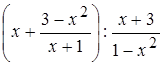, x=-299.

Докажите тождество: (18 баллов)

.

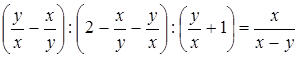III группа.

Составьте алгебраическую дробь, которая после сокращения будет равна 2.(2 балла)

Укажите значения переменных, при которых дробь: (5 баллов)

а) имеет смысл,

б) равна нулю.

.

Равны ли алгебраические дроби: (4 балла)

Познавательно о обучении:

Программа по изобразительному искусству для 5 класса
Содержание предметного блока «Изобразительное искусство» соответствует общим целям и задачам преподавания интегрированного курса «Искусство»: воспитание художественной культуры как части культуры духовной, приобщение школьников к миру изобразительного искусства, общечеловеческим и национальным ценн ...

Образовательная концепция Екатерины II и И.И. Бецкого
Первые серьезные шаги в деле организации женского образования были предприняты Екатериной II. Образовательная концепция Екатерины II и ее ближайшего сподвижника И.И. Бецкого пыталась педагогическими, образовательными средствами разрешить в кратчайшее время две крупнейшие социальные задачи: произвес ...

Особенности письменной речи
В связной письменной речи у детей выявляются большие трудности в установлении логических и языковых связей между предложениями. Последовательность предложений не всегда соответствует последовательности описываемых событий, нарушаются смысловые и грамматические связи между отдельными предложениями. ...