Обобщенная теорема синусов

Теорема 3.4: Биссектрисы трех внутренних углов треугольника конкурентны.

Окружность с центром в точке I и радиуса r касается всех трех сторон и поэтому является вписанной окружностью.

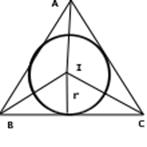
Вписанная и вневписанная окружности

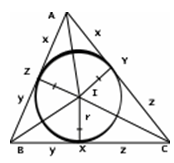
На рисунке изображена вписанная окружность, касающаяся сторон ВС, СА и АВ в точках X, Y, Z. Так как две касательные к окружности, проведенные из внешней точки, равны, то получаем, что |AY|=|AZ|, |BZ|=|BX|, |CX|=|CY|. На рисунке длины этих отрезков обозначены x, y, z так что y+z=a, z+x=b, x+y=c.

Складывая эти равенства и используя введенное Эйлером обозначение s для полупериметра (от «semiperimetr»), получим 2x+2y+2z= a + b + c=2s, поэтому x + y + z=s, т.е. справедлива.

Теорема 4.1: Для треугольника, изображенного на рисунке, выполняются соотношения:

x=s-a,

y=s-b,

z=s-c.

Так как треугольник IBC имеет основание равное а, высоту r, то его площадь равна: Прибавив к нему аналогичные выражения для и мы получим: следовательно, теорема доказана.

Теорема 4.2: Для треугольника, изображенного на рисунке, выполняется соотношение:

SABC = sr.

На рисунке изображен треугольник , стороны которого являются биссектрисами внешних углов треугольника АВС. Любая точка на биссектрисе угла В равноудалена от прямых АВ и ВС. Аналогично: любая точка на прямой равноудалена от прямых ВС и СА.

Следовательно, точка I, в которой эти биссектрисы пересекаются, находится на одинаковом расстоянии r от всех трех сторон. Так как I равноудалена от сторон АВ и АС, то она должна принадлежать множеству точек, равноудаленных от этих прямых, то есть она должна лежать на прямой А1, внутренней биссектрисе угла А.

Теорема 4.3: Внешние биссектрисы любых двух углов треугольника конкурентны с внутренней биссектрисой третьего угла.

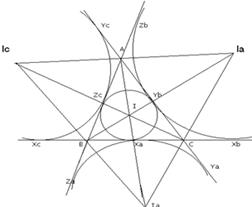
Окружность с центром в точке I радиуса r, касающаяся всех трех сторон треугольника, является одной из трех вневписанных окружностей. Каждая из вневписанных окружностей касается одной из сторон треугольника внутри, а двух других сторон (продолженных) извне.

Обозначив точки касания как на рисунке, две касательные из одной точки к окружности имеют одинаковые длины, то: ;

Следовательно, касательная из точки В (или любой другой вершины) к вневписанной окружности, расположенной за противолежащей стороной, имеет длину s. Действительно: .

Кроме того, так как: .

И так далее, то также и: .

3.5 Теорема Штейнера-Лемуса

Теорема 5.1: Любой треугольник, у которого равны длины биссектрис двух углов (измеряемые от вершины до противоположной стороны), является равнобедренным.

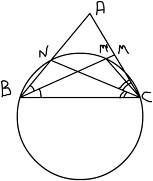
Одно из простейших доказательств этой теоремы опирается на следующие две леммы:

Лемма 5.1.1: Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.

Доказательство: Две равные хорды стягивают углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух неравных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно, меньший острый угол с вершинами на окружности.

Познавательно о обучении:

Общая характеристика внеучебной деятельности
Под внеучебной деятельностью понимается активное взаимодействие педагога с детьми, направленное на достижение определенных воспитательных целей. В процессе организации внеучебной деятельности у учащихся формируются предусмотренные новообразования или развиваются ранее приобретенные. В процессе их к ...

Технология триз как решение проблемы
Что же такое триз? Ответ прост – это уникальный инструмент для: - поиска нетривиальных идей, - выявления и решения многих творческих проблем, - выбора перспективных направлений развития техники, технологии и снижения затрат на их разработку и производство, - развития творческого мышления, формирова ...

Роль и место раздела в профильной подготовке школьников
Раздел "Информационные технологии" включен в образовательную область "Технология" не случайно. Понятия "информация" и "технология" являются неотъемлемой частью современной жизни. Информация – это не только сведения, передаваемые одними людьми другим, но и сам ...