Обобщенная теорема синусов

Лемма 5.1.2: В треугольнике с двумя различными углами меньший угол обладает большей биссектрисой.

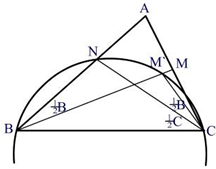
Доказательство: Пусть АВС – треугольник, в котором угол В меньше угла С, как на рисунке; пусть отрезки BM и CN делят пополам углы В и С. Мы хотим доказать, что |BM|>|CN|. Возьмем точку М` на отрезке ВМ так, чтобы ÐM`CN=1/2 ÐB. Так как это угол равен углу M`BN, то четыре точки N, B, C, M` на одной окружности.

Поскольку ÐB < 1/2(ÐB+ÐC) < 1/2(ÐA+ÐB+ÐC), то ÐCBN < M`CB <90°.

По лемме 5.1.1 |CN|<|M`B|. Следовательно, |BM|>|BM`|>|CN|.

Доказательство теоремы: Часто бывает, что теорема может быть выражена в форме «противоположной к обратной» – эквивалентной к обратной. Вместо доказательства теоремы 1.51 для нас будет достаточно доказать, что если в треугольнике АВС В ¹ С, то |BM| ¹ |CN|. Но это есть прямое следствие леммы 5.1.2.

Ортотреугольник

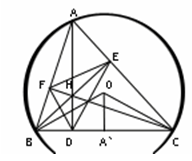
Теорема 6.1: Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

Одно из простейших доказательств опирается на две следующие леммы:

Лемма 6.1.1: Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.

Доказательство: Две равные хорды стягивают равные углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух неравных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно; меньший угол с вершиной на окружности.

Лемма 6.1.2: В треугольнике с двумя различными углами меньший угол обладает большей биссектрисой.

Доказательство: Пусть АВС – треугольник, в котором угол В меньше угла С, как на рисунке; пусть отрезки ВМ и CN делят пополам углы В и С. Мы хотим доказать, что . Возьмём точку М` на отрезке ВМ так, чтобы . Так как этот угол равен углу M`BN, то четыре точки N, B, C, M` лежат на одной окружности. Поскольку то . По лемме 6.1.1 . Следовательно,

Доказательство теоремы 6.1: Часто случается, что теорема может быть выражена в форме «противоположной к обратной» – эквивалентной первоначальной.

Вместо доказательства самой теоремы 6.1. нам достаточно доказать, что если в треугольнике АВС , то . Но это есть прямое следствие леммы 6.1.2.

Теорема 6.2: Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

Мы уже отметили на рисунке, что . А так как отрезок HD перпендикулярен отрезку DB, то и отрезок FD должен быть перпендикулярен отрезку OB. Перпендикулярность отрезков DE и OC, а также EF и OA показывается аналогично.

Познавательно о обучении:

Общая характеристика внеучебной деятельности
Под внеучебной деятельностью понимается активное взаимодействие педагога с детьми, направленное на достижение определенных воспитательных целей. В процессе организации внеучебной деятельности у учащихся формируются предусмотренные новообразования или развиваются ранее приобретенные. В процессе их к ...

Проблемы и перспективы развития дошкольного образования в Японии
В настоящий момент японское дошкольное образование не лишено разногласий и противоречий. В качестве первой проблемы можно указать на несогласие большинства родителей и педагогов с усилением частного сектора в дошкольном образовании, поскольку это приводит к снижению качества образовательных програм ...

Представление о психологической защите личности
В понимании психологической защиты на сегодняшний день в литературе отсутствует единое мнение. Первое упоминание о защите содержится в конце второй части "Предварительного сообщения" Бройера и Фрейда, представляющей собой один из разделов "Исследования по истерии". Впервые З. Фр ...