Применение софизмов на уроках математики

Итак, площадь фигуры, ограниченной синусоидой и осью Ох, равна нулю. Но площадь фигуры между некоторой кривой и осью Ох, может равняться нулю только в том случае, если эта кривая совпадает с осью Ох. Следовательно, график функции синус совпадает с осью Ох.

Раскрытие софизма:

Здесь допущена ошибка при интегрировании синуса. При вычислении с помощью интегрирования площади фигуры, заключенной между осью Ох и некоторой кривой, необходимо учитывать, что площадь при этом получается со знаком «плюс» или «минус». Это означает, что если кривая расположена над осью Ох, то площадь имеет знак «плюс», а если под осью Ох – знак «минус».

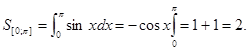Синус на отрезке [0; ] положителен, а на отрезке [] . Отрицателен. Поэтому площадь фигуры, заключённой между синусоидой и осью Ох, на отрезке [0; ] равна , а на отрезке [] площадь равна .

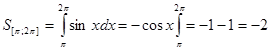Тогда площадь , на отрезке [0; 2] будет равна , а на отрезке [0; 2n] составит .

Софизмы могут самые разные и приведённая система подтверждает, что софизмы могут быть использованы и в соответствии с тематикой обучения, т.е. можно подобрать софизм, который будет актуален при проведении урока по различным темам. Конечно, разумно использовать софизм после изучения конкретной темы, например в 7 классе после темы «Формулы сокращённого умножения», или в 10 классе при изучении темы «Логарифмы», т.к. решение некоторых софизмов можно свести к тем же логарифмам или решить его, используя формулы сокращённого умножения.

Проработав соответствующую психолого-педагогическую и методическую литературу по данному вопросу, очевидно, сделать вывод о том, что критичность является важным качеством мышления, развитие которого требует значительных усилий со стороны учителя математики. Кроме того, полезно развивать критичность мышления, в процессе обучения, отступая от стандартных методов проведения урока.

Бесспорно, достичь поставленной цели с помощью только стандартных задач невозможно. Если учитель математики «заполнит отведённое ему время натаскиванием учащихся в шаблонных упражнениях, он убьёт их интерес, затормозит их умственное развитие». С помощью нестандартных задач интенсивнее формируется интерес и достигается цель углубления. Поиск решения нестандартных задач является прекрасным средством развития критического мышления, строгости суждений и математического вкуса. Одним из таких средств является использование софизмов на уроках математики.

Конечно, не следует, и преувеличивать роль софизмов в развитии критичности мышления. Они ни в коем случае не должны доминировать над обычными, традиционными упражнениями. Но как раз своей не стандартностью они «помогут» решить проблему заинтересованности в обучении, а если правильно организовать процесс внедрения софизмов в ход урока, то во многом облегчится задача развития критичности мышления, потому, что софизмы относятся к типам заданий, решение которых основано на рассмотрении различных ситуаций. При регулярном использовании софизмов на уроках у учеников вырабатывается своеобразная «подозрительность», что естественно указывает на хорошо развитую критичность мышления. Причём, софизмы универсальны в обучении тем, что подходят для учащихся всех возрастов.

Познавательно о обучении:

Контроль знаний и умений учащихся по физике
Контроль знаний и умений учащихся является важным звеном учебного процесса, от правильной постановки которого во многом зависит успех обучения. Выделяют следующие цели контроля знаний и умений учащихся: – диагностирование и корректирование знаний и умений учащихся; – учет результативности отдельног ...

Психолого-педагогические основы формирования начал экологической культуры у детей младшего дошкольного возраста
В переводе с греческого языка «экология» - это наука о доме, жилище («ойкос» - дом, «логос» - наука). Возникнув еще в прошлом веке как часть зоологии, экология определялась как наука о взаимоотношениях живых организмах с окружающей средой и друг с другом. Сейчас это направление называется биологиче ...

Факторы риска возникновения эмоциональных нарушений в детском возрасте
Спектр эмоциональных нарушений в детском и подростковом возрасте чрезвычайно велик. Это могут быть тяжёлые невротические конфликты, неврозоподобные состояния ребёнка вследствие органического поражения центральной нервной системы, преневротические состояния и др. В психологической литературе эмоцион ...