Организация деятельности учащихся по формированию геометрической грамотности

Анализ полученных данных показал, что на констатирующем этапе эксперимента успеваемость учащихся по первому уровню усвоения была _ %, но через достаточно малый промежуток времени выросла до _ %. Это говорит о том, что применение новых информационных технологий удовлетворяет первому из требований, предъявляемых образовательным процессом – обеспечению _% гарантии результата.

Для подтверждения достоверности отличий результатов в контрольной и экспериментальной группах нами был применен критерий согласия К.Пирсона. Данный выбор обоснован тем, что результаты эксперимента измерены с помощью шкал наименований.

Значение χ2 находится по формуле:

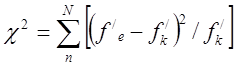(1)

где - относительная частота интервала экспериментальных данных;

- относительная частота интервала контрольных данных.

Проверим достоверность отличий результатов контрольной и экспериментальных групп по всем критериям формирования геометрической грамотности:

– способность выделять характерные свойства геометрических фигур;

– выполнять изображение фигуры по указанным свойствам;

– умение строить изображение геометрической фигуры по заданным величинам;

– умение находить решение геометрической задачи на вычисление, выполнив чертеж по условию задачи;

– выполнять необходимые дополнительные построения к заданному чертежу;

– способность выполнять измерения по готовым чертежам.

Для первого критерия - способность выделять характерные свойства геометрических фигур была построена рабочая таблица χ2 (см. таблицу _)

Таблица - Расчет χ2 по определению различий между группами для первого критерия.

Исходя из критических значений χ2 - критерия [Новиков Д.А. статистические методы в педагогических исследованиях (типовые случаи, М.: МЗ-Пресс, 2004, 67 с.)], при составляющих степенях свободы (n=2, т.к. интервалов 3), выясняем, что критическое значение χ2 с вероятностью _% равно _. Следовательно χ2emp> χ2krit95%, (34, 83> 6,0). Это подтверждает, что такие значения χ2 можно получить при случайном отборе учащихся с вероятностью более _ %.

Познавательно о обучении:

Мастерство учителя в управлении учебно-воспитательным процессом
Что должны знать студенты: формы и структуру групповых дел и групповой деятельности; приемы прогнозирования взаимодействия с воспитуемым; цели, задачи учебной работы и способы их реализации; взаимосвязь культуры педагогического труда и педмастерства на уроке. Что должны уметь студенты: управлять св ...

Урок – основная форма организации занятий с учащимися,отнесенными к специальной медицинской группе
Ученики, отнесенные к специальной группе, занимаются по особой программе. В ее основу проложено содержание общей программы, из практического раздела которой исключены средства физического воспитания, способные вызывать перенапряжения организма, например, физические упражнения, приводящие к максимал ...

Речь как основное средство педагогического взаимодействия. Развитие коммуникативных способностей педагога
Преподавателю слово дано не для того, чтобы усыпить свою мысль, а чтобы будить чужую. В.О. Ключевский Речь как основное средство педагогического взаимодействия 2. Упражнения на развитие фонационного дыхания 3. Упражнения на развитие голоса 4. Упражнения на развитие выразительности речи 5. Упражнени ...