Якоб Штейнер

В отличие от теоремы Ферма-Торричели, Штейнер рассматривал ту же проблему в несколько общем виде: он пытался найти кратчайшую сеть дорог, соединяющую три пункта.

Оказывается, что такая сеть должна состоять из трех сходящихся в одной точке прямолинейных дорог, причем, одна из этих дорог может сжаться в точку (как в задаче Ферма). Поставщики контейнеры рефрижераторы.

В такой формулировке, но уже для произвольного числа пунктов, задача приобретает и чисто практическое значение, например, ее приходится решать при прокладке кабельных сетей.

Если радиус катящейся окружности в. три раза меньше радиуса опорной, то точка описывает дельтоиду или кривую Штейнера (гипоциклоида с модулем m=3).

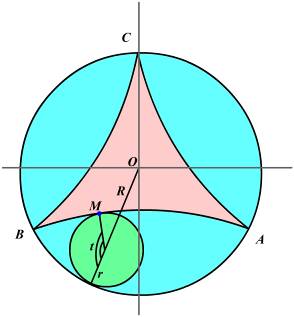
Уравнение кривой Штейнера в прямоугольной декартовой системе координат:

.

Имеются три точки возврата. Длина дуги от точки А: . Длина всей кривой . Радиус кривизны . Площадь, ограниченной кривой .

Познавательно о обучении:

Характеристика педагогического мастерства учителя
Профессия педагога – одна из важнейших в современном мире. От его усилий зависит будущее человеческой цивилизации. Профессиональный педагог - это единственный человек, который большую часть своего времени занимается воспитанием и обучением детей. Смысл педагогической профессии выявляется в деятельн ...

Нарушения связной речи
В работах многих авторов /М.Ф. Гнездилов, С.Н. Комской, Л.С. Вавиной, В.А. Гордиенко, С.Ю. Ильиной и др./ отмечается, что становление связной речи у умственно отсталых детей осуществляется замедленными темпами и характеризуется качественными особенностями. Они длительное время задерживаются на этап ...

Возможности дистанционного обучения в образовании взрослых
Широкое применение в системе образования информационных и телекоммуникационных технологий создало предпосылки для активного использования в учебном процессе дистанционного обучения (ДО). Этот термин, появившийся в отечественном педагогическом контексте сравнительно недавно, имеет англоязычные корни ...